Samuel is starting a business in the surveillance industry.
He provides closed IPTV surveillance systems to stores.
He aims to provide a reliable service but with a competitive price.
To achieve this he decided to add some limitations to the system:
Samuel is starting a business in the surveillance industry.
He provides closed IPTV surveillance systems to stores.
He aims to provide a reliable service but with a competitive price.
To achieve this he decided to add some limitations to the system:
Despite the budget limitations, Samuel also decided that he would use cameras with the ability to capture video in 360°.
Even with a functional system, Samuel continues with an unsolved problem: how to determine in which corner should the IPTV camera be installed? The only requirement is to install the camera in the corner that covers more area.
Samuel asked you to implement a solution that would help him. Each store can be represented by a simple polygon (whose boundary does not self-intersect), and each corner by a vertex. Consider that the polygons have no holes, meaning that nothing inside the store blocks the visibility of the camera, except an exterior wall. Observe the figure, which represents the data of sample 1.
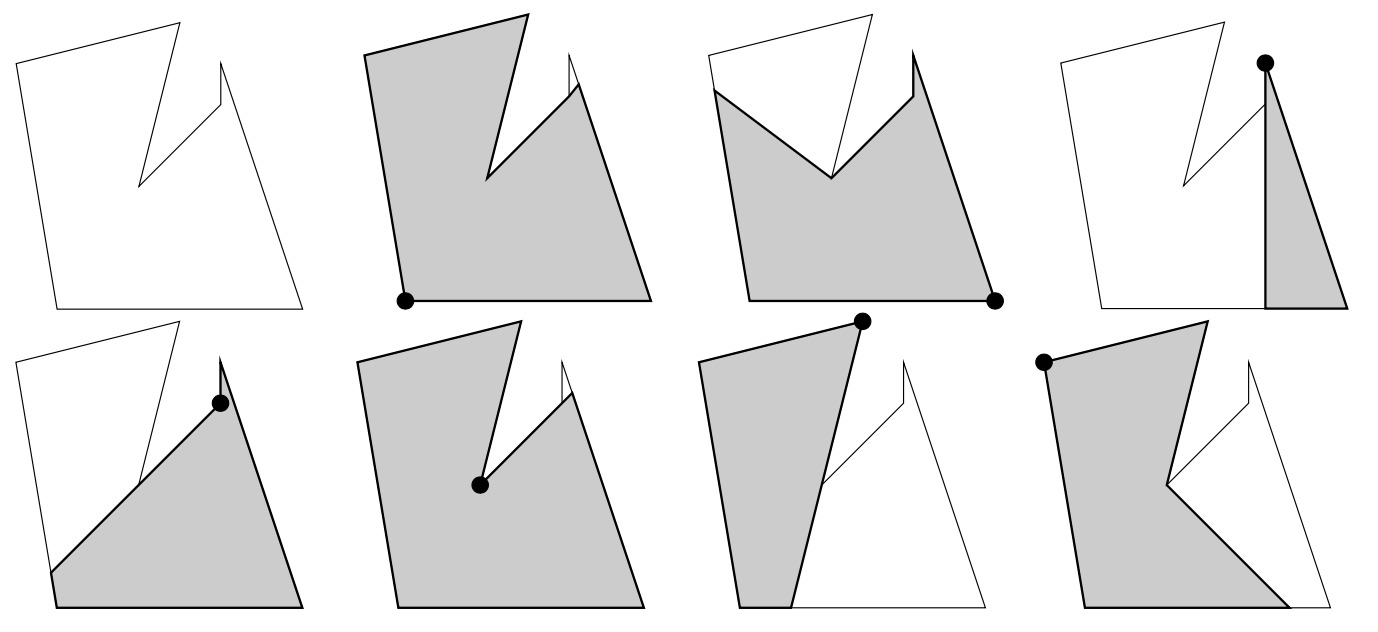
| Figure 1: Store representation and visibility polygons of each vertex |
Help Samuel to find the store corner where to install the camera.
The first line of the input has an integer n which indicates the number of vertices of the polygon that represents the store. The following n lines contain the coordinates x, y of the vertices of the polygon, listed in counterclockwise order. The coordinates’ values are integers and are separated by a space.
| 3 ≤ n ≤ 50 | Number of vertices |
| 0 ≤ x ≤ 500 | x coordinate of a vertex |
| 0 ≤ y ≤ 500 | y coordinate of a vertex |
The output has a single line with the coordinates, separated by a space, of the vertex that covers the largest area of the polygon, hence the one where the camera will be installed. In case the largest area is covered by two or more vertices, choose the vertex closest to the origin (w.r.t. the Euclidean distance). If there is still a tie (i.e., several vertices cover areas of largest size and are all at the same distance from the origin), choose the one closest to the x-axis.
7 1 0 7 0 5 6 5 5 3 3 4 7 0 6
1 0
4 0 0 1 0 1 1 0 1
0 0