Archaeologists have found that Sumerians kept their inventories on clay tablets using a pictorial representation. These representations include different symbols to denote different quantities in some metrological system. Different metrological systems were used for different types of goods.

Any metrological system contains several different-sized units with fixed conversion factors between them. For example, there are 12 inches in a foot, 3 feet in a yard, and so on. As in our old weight and measure systems, Sumerian metrology featured all sorts of conversion factors.

In the basic sexagesimal system used for counting sheeps, cows, fish:

• a single entity was denoted by a small cone;
• 10 cones equalled one small circle;
• 6 small circles equalled one big cone;
• 10 big cones equalled one big cone with a circle inside it;
• 6 big cones with a circle inside equalled one large circle; and
• 10 large circles equalled one large circle with a small circle inside.
  (This last unit was then worth 10 x 6 x 10 x 6 x 10 = 36000 base units.)

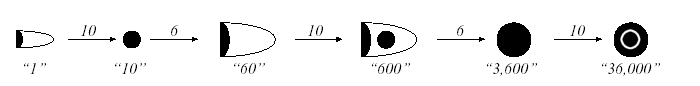
For discrete ration goods, a 'bisexagesimal' system was used with conversion factors 10, 6, 2, 10, and 6.

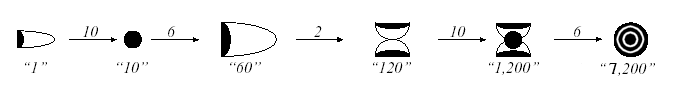
Yet another system was used for measuring grain capacity, with conversion factors 5, 10, 3, and 10.

Some tablets contain several entries of counted objects in one surface and the corresponding summation on the reverse surface (c.f. the figure on the right). Due to these tablets, the conversion factors of the various systems could have been found out. Basically, your task is to write a program that, given such an addition, finds the conversion factors of the system.

An metrological alphabet A is a non-empty sequence of distinct symbols, in strictly increasing order of the number of goods they represent. The first symbol is the base unit and is worth 1.

A number over the alphabet A is a sequence of symbols from A whose represented value cannot be obtained by any other sequence of symbols from A with a smaller length.

For example, if the first three symbols of a metrological alphabet are '&', '@' and '$', and the corresponding conversion factors are 4 and 3:

• the sequences '&@' and '@&' are numbers, both denoting the value 5, but '&&&&&' is not a number.
• the value 14 can only be written as a sequence with one symbol '$' and two symbols '&', in any order.

Given a metrological alphabet A and three numbers x, y and s over A, such that s is the sum of x and y, find all the conversion factors that can be inferred from the addition.

Input

The input consists of four lines.

The first line contains an alphabet with N distinct symbols (1 <= N <= 100).

Each of the following three lines contains a number, whose length (number of symbols) varies between 1 and 200. The last number is the sum of the first two.

Output

The output consists of a single line that contains a sequence of 2N - 1 elements, separated by a space.

The sequence alternates the symbols of the alphabet (in the given order) and the information that can be inferred about the corresponding conversion factors. That information is the conversion factor, if it can be determined, or the symbol '?', otherwise.

For instance, in the example below:

• 2 symbols 'O' equal one '#';
• 3 symbols '#' equal one 'Ø';
• 4 symbols '+' equal one '*';
• but neither the conversion factor between 'Ø' and 'S' nor the conversion factor between 'S' and '+' can be deduced from the addition.

O#ØS+*
+++SØØ##O
+Ø#O#
*SØØØØ##

O 2 # 3 Ø ? S ? + 4 *