Problem C

Rectangle by the Ocean

Some countries are literarily known by their shapes. For example, France is sometimes referred to as ‘the hexagon’, Italy is called ‘the boot’ and Portugal is known as ‘the rectangle by the ocean’ (the Atlantic Ocean, of course).

Given our mathematical background, we are curious to know exactly which rectangle we are talking about when we say that Portugal is a rectangle. More precisely, we want to compute the rectangle that best fits the contour of the Portuguese map (not counting the islands). By definition, that would be a rectangle with horizontal basis for which at least three of the four corners lie on the contour of the map and whose area is closest to the area of the map (either from above or from below).

Problem

In general, we are given a closed line on a plane, which we shall call here a ‘contour’ (see below for a better characterization of our contours), and we want to discover a rectangle with horizontal and vertical sides having at least three of the four corners on given points of the contour and such that its area is closest to the area inside the contour.

For this task, each contour is described by a sequence of contiguous segments, each segment connecting a point with integer coordinates to one of the eight points with integer coordinates nearby, horizontally, vertically, or diagonally. The contour is closed and does not touch itself. Here is an example, whose area is 12.5:

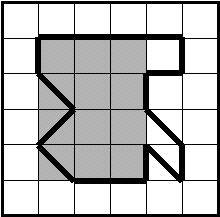
This figure corresponds to the data presented in the Sample Input and Sample Output sections below (assuming the lower left corner of the grid has coordinates (0, 0)). The shaded area represents the solution.

Input

The first line of the input file contains one integer, N, representing the number of points that define the contour, 4 <= N <= 256.

Each of the N following lines contains two integers, X and Y, separated by a space, defining the x and y coordinates of a point along the contour. Note that X and Y can be positive, negative or zero.

Successive points P_i and P_i+1 (with 1 <= i < N) define a segment that belongs to the contour. The last segment is defined by P_N and P₁, thus closing the contour. The x coordinates of P_i and P_i+1 and also of P_N and P₁ differ by at most 1 (in absolute value) and so do the y coordinates. All points are distinct.

Output

The output file has two lines. The first line contains one number: the area within the contour, written with exactly one decimal place; the second line contains four integers, separated by a space: the coordinates of the lower left corner and of the upper right corner of the computed rectangle.

The computed rectangle has at least three of its four corners on the points given to define the contour and its area is as close as possible to the area within the contour.

If more than one rectangle meets these requirements, your program should provide the one whose sequence of coordinates is lexicographically the least.

Sample Input

17
1 2
2 3
1 4
1 5
2 5
3 5
4 5
5 5
5 4
4 4
4 3
5 2
5 1
4 2
4 1
3 1
2 1

Sample Output

12.5
1 1 4 5

---

MIUP'2004: Fourth Portuguese National Programming Contest

---