We consider sequences formed from the addition of terms of a given
sequence. Let 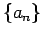 ,
,
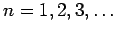 , be an arbitrary
sequence of integer numbers;
, be an arbitrary
sequence of integer numbers; 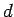 a positive integer. We construct
another sequence
a positive integer. We construct
another sequence 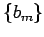 ,
,
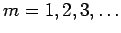 , by defining
, by defining 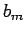 as consisting of
as consisting of
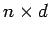 occurrences of the term
occurrences of the term 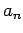 :
:
For example, if 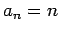 , and
, and 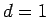 , then the resulting sequence
, then the resulting sequence 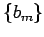 is:
is:
Problem
Given 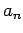 and
and 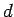 we want to obtain the corresponding
we want to obtain the corresponding 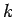 th
integer in the sequence
th
integer in the sequence 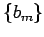 . For example,
with
. For example,
with 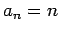 and
and 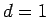 we have 3 for
we have 3 for 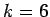 ;
we have 4 for
;
we have 4 for 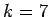 . With
. With 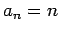 and
and 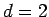 ,
we have 2 for
,
we have 2 for 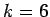 ; we have 3 for
; we have 3 for 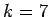 .
.
Input
The input consists of three lines:
- The first line represents
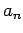 -
a polynomial in
-
a polynomial in 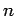 of degree
of degree 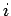 with non-negative integer coefficients in increasing
order of the power:
where
with non-negative integer coefficients in increasing
order of the power:
where
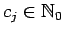 ,
,
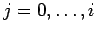 .
This polynomial
.
This polynomial 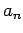 is codified by its degree
is codified by its degree 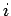 followed by the coefficients
followed by the coefficients 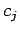 ,
,
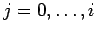 .
All the numbers are separated by a single space.
.
All the numbers are separated by a single space.
- The second line is the positive integer
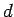 .
.
- The third line is the positive integer
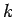 .
.
It is assumed that the polynomial 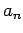 is a polynomial of degree less or equal than 20 (
is a polynomial of degree less or equal than 20 (
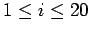 )
with non-negative integer coefficients less or equal than 10000
(
)
with non-negative integer coefficients less or equal than 10000
(
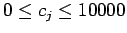 ,
,
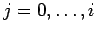 );
);
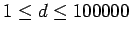 ;
;
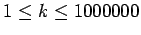 .
.
Output
The output is the 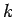 th integer in the sequence
th integer in the sequence 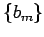 .
This value is less or equal than
.
This value is less or equal than 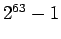 .
.
Sample Input
4 3 0 0 0 23
25
100
Sample Output
1866
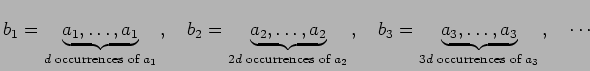
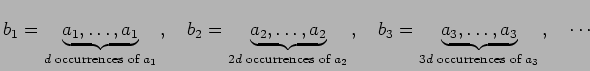
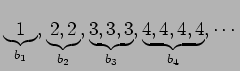
![]() and
and ![]() we want to obtain the corresponding
we want to obtain the corresponding ![]() th
integer in the sequence
th
integer in the sequence ![]() . For example,
with
. For example,
with ![]() and
and ![]() we have 3 for
we have 3 for ![]() ;
we have 4 for
;
we have 4 for ![]() . With
. With ![]() and
and ![]() ,
we have 2 for
,
we have 2 for ![]() ; we have 3 for
; we have 3 for ![]() .
.
![]() is a polynomial of degree less or equal than 20 (
is a polynomial of degree less or equal than 20 (
![]() )
with non-negative integer coefficients less or equal than 10000
(
)
with non-negative integer coefficients less or equal than 10000
(
![]() ,
,
![]() );
);
![]() ;
;
![]() .
.
![]() th integer in the sequence
th integer in the sequence ![]() .
This value is less or equal than
.
This value is less or equal than ![]() .
.