Problema A

Base Lunar

A PASSA (Portuguese Air Space Special Agency) recebeu um contrato dos americanos para estudar possíveis locais de aterragem na lua (ou alunagem) para o vaivém espacial. Como sabemos, o vaivém aterra como um avião e precisa de uma pista bastante longa. O problema é que a lua está cheia de crateras e é difícil arranjar um pedaço de terreno suficientemente comprido e sem obstáculos para aí construir a base lunar para o vaivém.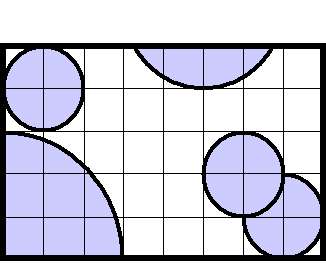

Felizmente, a superfície da lua já está bem estudada e existem mapas muito detalhados. Para este projecto, a PASSA vai usar um mapa de uma secção rectangular da superfície lunar, onde estão claramente assinaladas as crateras. Em virtude de fenómenos astronómicos que ultrapassam a nossa compreensão, todas as crateras são rigorosamente circulares. Há crateras dentro de crateras e até há crateras que se intersectam. O mapa está dividido em quadrículas cujo lado é uma unidade de comprimento lunar, e isso determina um referencial cuja origem está no canto inferior esquerdo do rectângulo (o canto mais a sudoeste), com o semi-eixo positivo dos x para a direita (isto é, para leste) e o semi-eixo positivo dos y para cima (isto é, para norte). O centro de cada cratera é um ponto de coordenadas inteiras neste referencial, mas pode haver crateras cujo centro esteja fora do mapa ou cujo centro esteja no mapa mas em que a circunferência da cratera esteja parcialmente (ou totalmente) fora do mapa.

A figura representa um mapa onde vemos três crateras inteiras e duas outras apenas parcialmente.

O problema é descobrir as localizações que permitam construir as pistas de alunagem mais compridas que for possível, na direcção esteoeste e na direcção norte-sul.

Tarefa

A sua tarefa é escrever um programa para calcular as coordenadas e o comprimento das pistas mais compridas, na horizontal e na vertical, que se podem construir na região da lua representada num mapa com as características indicadas. As pistas têm de estar fora das crateras e serão formadas por conjuntos de quadrículas justapostas na mesma direcção (horizontal ou vertical). Para efeitos dos cálculos, considera-se que uma quadrícula está fora da cratera se o seu centro não pertencer ao círculo da cratera. Note bem: a circunferência da cratera faz parte da cratera.

Dados

O mapa da lua vem representado num ficheiro, acessível através do standard input. A primeira linha do ficheiro tem dois números inteiros L e H, 0 < L <= 20, 0 < H < 20 representado a largura e a altura do mapa. Na segunda linha vem um número inteiro N, representando o número de crateras, 0 <= N <= 50. Seguem-se N linhas cada uma com três números inteiros X, Y e R, onde X e Y representam as coordenadas do centro da cada uma das N crateras e R o respectivo raio.

Note que as coordenada dos centros das crateras podem estar fora do mapa. Em particular, podem ser negativas. O raio é um número inteiro positivo.

Resultados

O ficheiro de saída, associado ao standard output, contém duas linhas, cada uma com três números inteiros separados por um espaço. Em cada linha, os dois primeiros números representam as coordenadas do canto inferior esquerdo da quadrícula onde a maior pista possível começa e o terceiro representa o comprimento dessa pista. Cada pista possível tem duas extremidades, mas dizemos que a pista começa na extremidade mais próxima do canto inferior esquerdo do mapa. A primeira linha diz respeito à maior pista na direcção este-oeste e a segunda à maior pista na direcção norte-sul. Em caso de empate, isto é, se houver várias pistas possíveis com o mesmo comprimento máximo, numa dada direcção, prefere-se a que começa mais a sul e se houver duas ou mais que comecem igualmente a sul, prefere-se a que começa mais a oeste.

No caso de não haver solução (porque as crateras cobrem tudo) ambas as linhas devem ter três zeros.

Exemplo de ficheiro de dados

Exemplo de ficheiros de resultados

2 3 6
3 0 5