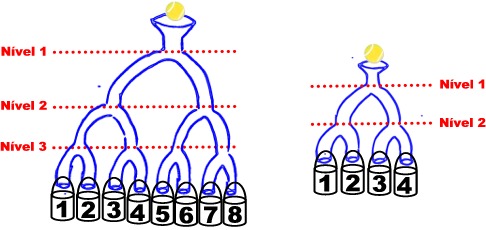
Figura 1 - TUGA de 3 níveis e TUGA de 2 níveis
O famoso inventor e professor Orlando Nuno Isildo (Prof. O.N.I.) é conhecido por inventar todo o tipo de máquinas sem utilidade aparente mas que despertam novas tecnologias que mais tarde poderão criar uma nova era.
Sempre que os seus 5 sobrinhos o visitam no laboratório, uma máquina merece a sua especial atenção: a máquina de Tubos Unidos pela Gravidade Anárquica (T.U.G.A.). A sua concepção é muito simples. A TUGA tem uma série de tubos com ramificações. Mais precisamente, começa por um único tudo que depois se bifurca em dois, cada uma destas ramificações divide-se novamente por dois tubos e assim sucessivamente como exemplificado na figura 1. No final de cada tubo encontramos um balde, e os baldes são todos numerados, da esquerda para a direita, começando no 1.

Figura 1 - TUGA de 3 níveis e TUGA de 2 níveis
A TUGA tem um tamanho definível pelo Prof. ONI, pois ele tem várias cópias de bifurcações que podem ser montadas umas em cima das outras. Para definirmos uma TUGA basta dizermos quantos níveis tem, ou seja, quantas vezes os tubos se ramificam em dois. A figura 1 mostra uma TUGA de 3 níveis e uma TUGA de 2 níveis.
A ideia é lançarmos uma bola no início do primeiro tubo e esperar para ver em que balde a bola cai, puxada pela força da gravidade. Para tornar a TUGA imprevisível, o Prof. ONI instalou umas pequenas patilhas em cada bifurcação que fazem a bola ir para a esquerda ou para a direita, como exemplificado na figura 2.
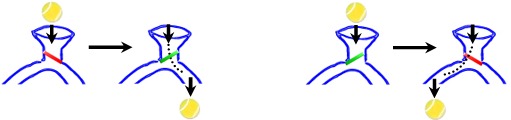
Figura 2 - Funcionamento das patilhas
Todas as patilhas estão inicialmente numa posição em que a bola vai para a direita. Quando a bola passa numa patilha, segue a direcção imposta por esta mas muda a posição da patilha. Portanto, depois de uma bola lançada, todas as patilhas do caminho que percorreu trocaram de posição. A título de exemplo, a figura 3 ilustra o que acontece se atirarmos 4 bolas numa TUGA de dois níveis.
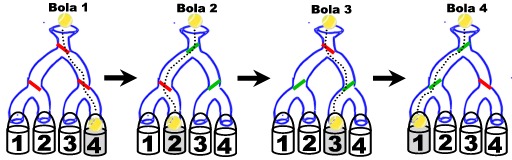
Figura 3 - 4 bolas atiradas numa TUGA de 2 níveis
Os sobrinhos do Prof. ONI gostam de atirar muitas bolas porque nunca sabem onde estas vão parar. No entanto, o sobrinho mais velho está convencido que consegue descobrir exactamente em que balde cai cada bola e resolveu pedir-te ajuda.
A tua tarefa é escrever um programa que descobre em que balde cai a N-ésima bola (a bola número N) numa TUGA de um dado nível. Relembra que quando se atira a primeira bola, a TUGA tem sempre todas as patilhas na posição que faz a bola ir para a direita numa bifurcação.
Na primeira linha do input vem um número C que representa o número de casos a considerar.
Cada caso é representado por uma linha contendo dois números inteiros separados por um espaço, L N, onde L representa o número de níveis da TUGA a considerar (1 < L < 20) e N representa que queremos saber onde cai a bola número N (1 ≤ N ≤ 1 000 000).
Para cada linha de input vem uma linha de input, contendo um único número inteiro, que indica qual o número do balde onde a bola número N cai numa máquina de L níveis.
6 2 1 2 2 2 3 2 4 2 5 3 3
4 2 3 1 4 6