Problem F - The Bridges of Kölsberg

Background

King Beer has a very hard region to rule, consisting of lots of cities with very sectarian operating system beliefs and high levels of trade. These cities are placed along a river, the Kölsberg, along its Northern and Southern banks. The cities are economically separated from each other, since the river is wide and dangerous.

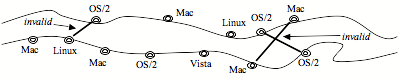
A section of the Kölsberg showing some invalid bridges

King Beer would like to build some bridges connecting opposite banks of the river. He was strongly advised against making bridges between cities with different operating systems beliefs (those guys really hate each other). So, he is just going to build bridges between cities sharing the same operating system belief (even if the resulting bridges are quite long and strangely shaped). However, it is technical impossible to build bridges that cross other bridges.

The economical value of a bridge is the sum of the trade values the two cities it connects. The King wants to maximize the sum of all possible bridge values while minimizing the number of bridges to build.

Problem

Given two sets of cities, return the maximum possible sum of all bridge values and the smallest number of valid bridges necessary to achieve it.

Input

The first line is an integer with the number of samples. For each sample, the next line has a non-negative integer, not greater than 1,000, indicating the number of cities on the Northern riverbank. Then, on each line, comes the city information with the form

cityname ostype tradevalue

where, separated by empty spaces, there are two strings, cityname and ostype, with no more than 10 characters each, and tradevalue which is a non-negative integer not greater than 10⁶. The sequence of lines represents the cities from left to right along the riverbank. Next, there is the same kind of information to describe the Southern riverbank.

Output

For each sample, a line consisting of the maximum possible sum of all bridge values, one empty space, the number of bridges.

Sample Input

1
3

mordor Vista 1000000

xanadu Mac 1000

shangrila OS2 400

4

atlantis Mac 5000

hell Vista 1200

rivendell OS2 100

appleTree Mac 50

Sample Output

1002250 2