Problem D: Where are the Squares?
The Hough Transform (HT) is a method for detecting linear structures in images. It can be used to isolate features of a particular shape within an image. Commonly it is used in image processing to detect lines. Lines can be represented in Cartesian space using the equation
For computational purposes it is sometimes better to use Polar Coordinates in the equation
|
y = | ⎛
⎝
|
− |
cos θ
sin θ
| ⎞
⎠
|
x+ | ⎛
⎝
|
r
sin θ
| ⎞
⎠
|
|
|
This can be rearranged in the form of a Hough Space (r, θ):
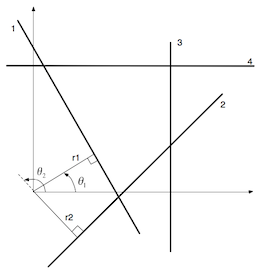
Using this equation every line can be described as a combination of (r, θ), where r is the length of the normal vector that connects the line to the origin and θ is the angle of vector r. In order to be able to represent all possible lines the angle varies in the interval [0°,180°[ (values in degrees, not radians) and r is negative whenever it is bellow the abscissa. Example:
Line 1: r1 = 10, θ1 = 30°
Line 2: r2 = −8, θ2 = 135°
Line 3: r3 = 25, θ3 = 0°
Line 4: r4 = 23, θ4 = 90°
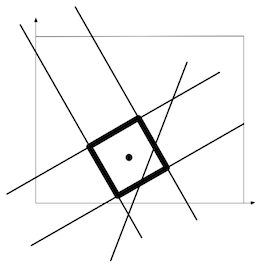
Given an image with a set of detected lines in Hough Space (no repeated lines), it is possible to detect all squares in the image as seen in the example:
Task
Given an image with width W, height H and a set of L detected infinite straight lines, return the number of regular squares S in which the center of the square is inside the image. This means that for each square center (cx,cy) the following conditions apply: 0 ≤ cx < W and 0 ≤ cy < H.
Input
The first line consists of three integers, W and H the width and height of the image and L, the number of lines. Then L lines follow, in each line there are two integers ri and θi, representing the Hough parameters of each line.
Output
The output consist of a single line containing S, the number of squares with center inside the image.
Constraints
- 0 ≤ W,H ≤ 2000
- 0 ≤ θi < 180
- 0 < L ≤ 1000
Input example 1
100 100 6
42 83
5 173
54 83
33 82
27 68
-7 173
Output example 1
1