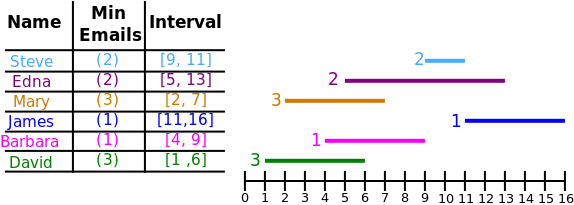Problem H: Problem Setters
 Amy is organizing a programming contest and she is the leader of the scientific committee, whose main responsibility is the creation of the problem set. Amy has a strict deadline for the initial proposal of problems but she knows that without sending emails remembering the deadline some of the members of the committee will forget about the contest. She wants to send the fewest possible number of emails, but she also knows that not all dates are equally effective for this task: send a message too soon and some of the members will forget about the contest; send a message too late and some will not have enough time. Since Amy knows all members very well from previous contests, she can estimate what is the minimum number of emails each person should receive and in which interval of time she should reach each of them.
Amy is organizing a programming contest and she is the leader of the scientific committee, whose main responsibility is the creation of the problem set. Amy has a strict deadline for the initial proposal of problems but she knows that without sending emails remembering the deadline some of the members of the committee will forget about the contest. She wants to send the fewest possible number of emails, but she also knows that not all dates are equally effective for this task: send a message too soon and some of the members will forget about the contest; send a message too late and some will not have enough time. Since Amy knows all members very well from previous contests, she can estimate what is the minimum number of emails each person should receive and in which interval of time she should reach each of them.
Imagine for instance the following scenario with six members of the committee (besides Amy) and their respective minimum number of emails and intervals:
Every time Amy sends an email, all committee members will be put as recipients. Knowing that she will never send more than one email per day, she needs to decide on which days she should send a message. The figure below shows three different valid possibilities, all of them respecting both the minimum number of emails and intervals of each person. Out of these three possibilities Amy prefers the last one, which requires less emails than the other two.
Note that the last alternative is an optimal solution
because, in this example (which corresponds to sample 1),
Amy needs to send at least 5 emails.
Can you help Amy decide what is the minimum number of emails needed?
Task
Given N ki values and intervals [ai, bi], indicating that the i-th member of the committee needs to receive a minimum of ki emails between days ai and bi (inclusive) before the deadline, your task is to determine the smallest number of days in which Amy needs to send an email so that every member will receive at least ki emails on its corresponding interval.
Input
The first line of the input contains N, the number of members of the committee. The following N lines contain each one three integer values,
ki, ai and bi, indicating the minimum amount of emails (ki) and interval [ai, bi] for the i-th committee member.
Constraints
| 1 ≤ N ≤ 35 000 | Number of members of the scientific committee
|
| 1 ≤ ki ≤ 5 | Minimum amount of emails per person
|
| 1 ≤ ai ≤ bi ≤ 109 | Days of each interval (with bi − ai + 1 ≥ ki)
|
Output
The output should consist of
a single line with an integer indicating the minimum number of emails needed.
Sample Input 1
6
2 9 11
2 5 13
3 2 7
1 11 16
1 4 9
3 1 6
Sample Input 2
8
1 20 20
2 5 7
1 7 9
2 4 8
1 3 5
1 2 3
1 9 10
4 15 18
 Amy is organizing a programming contest and she is the leader of the scientific committee, whose main responsibility is the creation of the problem set. Amy has a strict deadline for the initial proposal of problems but she knows that without sending emails remembering the deadline some of the members of the committee will forget about the contest. She wants to send the fewest possible number of emails, but she also knows that not all dates are equally effective for this task: send a message too soon and some of the members will forget about the contest; send a message too late and some will not have enough time. Since Amy knows all members very well from previous contests, she can estimate what is the minimum number of emails each person should receive and in which interval of time she should reach each of them.
Amy is organizing a programming contest and she is the leader of the scientific committee, whose main responsibility is the creation of the problem set. Amy has a strict deadline for the initial proposal of problems but she knows that without sending emails remembering the deadline some of the members of the committee will forget about the contest. She wants to send the fewest possible number of emails, but she also knows that not all dates are equally effective for this task: send a message too soon and some of the members will forget about the contest; send a message too late and some will not have enough time. Since Amy knows all members very well from previous contests, she can estimate what is the minimum number of emails each person should receive and in which interval of time she should reach each of them.