Problema D: E, de resto?

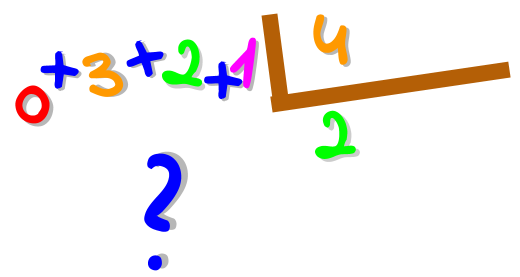
Realizam-se este ano na Abobadeira as finais nacionais das Olimpíadas da Numerologia, cujo evento principal é o Jogo do Resto. Nós vamos apoiar com a programação do quadro de resultados e precisamos da vossa colaboração. Ainda não conhecem o Jogo do Resto? É muito simples:

  1. joga-se com \(N\) jogadores, do jogador \(0\) ao \(N-1\);
  2. cada jogo tem \(M\) jogadas;
  3. em cada jogada, cada jogador regista um número inteiro de \(0\) a \(N-1\);
  4. somam-se os números registados por todos os jogadores, \(S\);
  5. calcula-se o resto \(R\) da divisão inteira de \(S\) por \(N\), com \(0\leq R \leq N-1\);
  6. o jogador com o número \(R\) contabiliza mais 1 ponto, os restantes mantêm os que têm;
  7. no final das \(M\) jogadas ganha quem totalizar mais pontos.

Tarefa

Escreva um programa para ler as várias jogadas, contabilizar os pontos dos jogadores e indicar os vencedores.

Input

A primeira linha tem dois inteiros: \(N\) (o número de jogadores) e \(M\) (o número de jogadas). Seguem-se \(M\) linhas contendo as jogadas. Cada linha com uma jogada contém \(N\) inteiros \(J_0, J_1, \ldots J_i, \ldots J_{N-1}\), com \(0 \leq i < N\) e \(0 \leq J_i < N\).

Restrições

\(1\leq N < 100\) Número de jogadores
\(1 \leq M < 100\) Número de jogadas

Output

O resultado consiste em 2 grupos de linhas, cada linha com apenas um inteiro. As linhas do primeiro grupo têm o total de pontos de cada jogador, por ordem crescente do número do jogador. Entre o primeiro e o segundo grupo de linhas há uma linha em branco. As linhas do segundo grupo apresentam os números dos jogadores que totalizaram o maior número de pontos e por isso venceram o jogo, também por ordem crescente do seu número.

Exemplo 1

Input 

2 4 
0 0 
0 1 
1 0 
1 1

Output 

2
2

0
1

Exemplo 2

Input 

3 5 
0 1 2 
2 1 0 
0 0 0 
1 1 2 
0 2 0

Output 

3
1
1
 
0


ToPAS'2016