Note: When developing objects without mutable state, that is in a functional style, the identity requirement is dropped. Changing the "state" of an object amounts to creating a modified copy of it. The individuality of the objects becomes blurred, but it is still the objects that are in charge of the computation.
The O-O paradigm simplifies the process of producing extensible code. An extensible system is a system that you can grow and adapt, without having to change what has already been written.
Really extensible code requires the programmer to write code as abstract as possible. Code written based on abstract concepts is able to deal with the original entities described in the statement of the problem, and also with new entities to be created in the future. Of course, this only works if those future entities conform with the abstractions initially considered.
class Point2(xc: Int, yc: Int) { // xc and yc are the "constructor arguments
var x: Int = xc
var y: Int = yc
def shift(that: Point2) = {
x += that.x
y += that.y
}
override def equals(that: Any) = {
that match {
case t: Point2 => x == t.x && y == t.y
case _ => false
}
}
override def toString(): String = "(" + x + ", " + y + ")";
}
class Point3(xc: Int, yc: Int, zc: Int) extends Point2(xc, yc) {
var z: Int = zc
def shift(that: Point3) = {
super.shift(that) ;
z += that.z
}
override def equals(that: Any) = {
that match {
case t: Point3 => super.equals(t) && z == t.z
case _ => false
}
}
override def toString(): String = "(" + x + ", " + y + ", " + z + ")";
}
scala> val p = new Point2(1,2)
p: Point2 = (1, 2)
scala> p
res3: Point2 = (1, 2)
scala> println(p)
(1, 2)
scala> p shift p ; println(p)
(2, 4)
scala> val q = new Point2(5,5)
p: Point2 = (5, 5)
scala> val r = new Point2(5,5)
r: Point2 = (5, 5)
scala> q.equals(r) // equality
res9: Boolean = true
scala> q == r // equality
res9: Boolean = true
scala> q eq r // identity
res9: Boolean = false
scala> val z = new Point3(0,0,0)
r: Point3 = (0, 0, 0)
scala> z shift r ; println(s) // uses the inherited method
(5, 5, 0)
scala> r shift z ; println(r) // Point3 is a subtype of Point2
(10, 10)
scala> var x: AnyRef = new Point3(0,0,0)
x: AnyRef = (0, 0, 0)
For a contrast, see a complete implementation of Rational numbers without state, here [E:31].
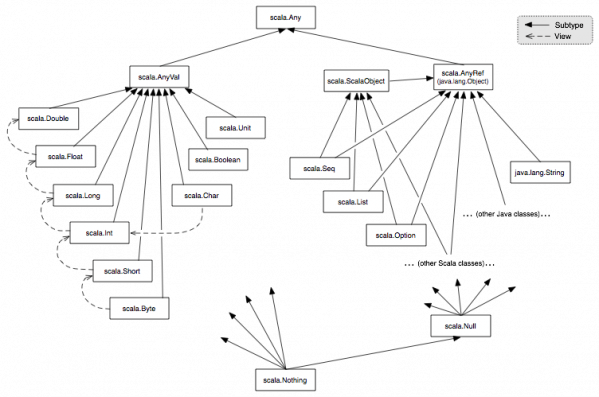
Study the following classes:
All the details are in [F:139-156] (chapter 12).
All the details are in [E:31-36] (chapter 6).
Typically, a trait defines a general behavior or a general feature that may be added to a new class when the class is defined. A useful trait is one that might apply to many different, usually unrelated, classes. Inheriting from a mixin is not a form of specialization but is rather a means of incorporating some new functionality. So, the role of a trait is quite different form the role of an abstract class.
We know how to define a new concrete subclass B that extends an existing superclass A. But the new features in the subclass B cannot be reused to extend a different superclass than A. A trail is a generic subclass that in parametrized in its superclass, and therefore can be reused to extend different superclasses.
A trait contains:
Interfaces in Java solve the problems of subtyping and conceptual modeling within the context of single inheritance, but does not allow code reuse. Traits allow code reuse and, at the same time, avoid the many problems of multiple inheritance.
A class can incorporate multiple traits using the with keyword, accumulating their implementations. Example:
class SuperCar extends Car with Flying with Diving
The traits can also be mixed-in when creating a new object. Example:
val supercar = new Car with Flying with Diving
Another example: we can add comparison operators to our Point3 class by mixing-in the predefined trait Ordered, as follows:
class Point3(xc: Int, yc: Int, zc: Int) extends Point2(xc, yc) with Ordered[Point3] {
def compare(that: Point3) = { ... }
...
}
The predefined trait Ordered is defined like this:
trait Ordered[A] {
// requires
def compare(that: A): Int
// provides
def < (that: A): Boolean = (this compare that) < 0
def > (that: A): Boolean = (this compare that) > 0
def <= (that: A): Boolean = (this compare that) <= 0
def >= (that: A): Boolean = (this compare that) >= 0
def compareTo(that: A): Int = compare(that)
}
The traits are mixed sequentially, and the later ones become dominant. So, there is never any ambiguity in the inheritance path, when names are reused. Study this example:
scala> trait T {
def f = { println("T") }
}
defined trait T
scala> trait A extends T {
override def f = { println("A") ; super.f }
}
defined trait A
scala> trait B extends T {
override def f = { println("B") ; super.f }
}
defined trait B
scala> (new AnyRef with A with B).f
B
A
T
scala> (new AnyRef with B with A).f
A
B
T
abstract class Expr {
def eval: Int
}
class Number(n: Int) extends Expr {
def eval: Int = n
}
class Sum(e1: Expr, e2: Expr) extends Expr {
def eval: Int = e1.eval + e2.eval
}
But if the types of the data don't change and we want to build systems that should be extensible with new operations, be better approach is to use the old idea of algebraic data types, with the associated notions of constructor and pattern matching (a selection and decomposition mechanism).
Scala supports directly the idea of algebraic data types via the notion of case class. Example:
abstract class Expr
case class Number(n: Int) extends Expr
case class Sum(e1: Expr, e2: Expr) extends Expr
def eval(e: Expr): Int = e match {
case Number(x) => x
case Sum(l, r) => eval(l) + eval(r)
}
The extern function can be stored as a method inside the abstract class,
abstract class Expr {
def eval: Int = this match {
case Number(n) => n
case Sum(e1, e2) => e1.eval + e2.eval
}
}
case class Number(n: Int) extends Expr
case class Sum(e1: Expr, e2: Expr) extends Expr